Automated dielectrophoretic characterization of <named-content content-type="genus-species" type="simple">mycobacterium smegmatis</named-content>

Automated Dielectrophoretic Characterization of Mycobacterium smegmatisBenjamin G. Hawkins,† Chao Huang,† Srinitya Arasanipalai,‡ and Brian J. Kirby*,‡†Department of Biomedical Engineering, and ‡Sibley School of Mechanical and Aerospace Engineering,Cornell University, Ithaca, New York, United States We report the positive dielectrophoretic (pDEP) characterization of wild-type and ethambutol-treated Mycobacterium smegmatispopulations via automated pDEP cell trapping experiments. The automated technique was validated by measurements ofcarboxylate-modified polystyrene microspheres and Escherichia coli. The characterization of M. smegmatis identifies a key frequencyregime where the membrane-specific action of ethambutol leads to a change in the cellular dielectrophoretic response. This workrepresents the first such characterization of Mycobacteria and highlights the potential for DEP measurements to measure changes inmycobacterial membrane properties associated with chemical treatments or genetic mutation.
Dielectrophoresis (DEP) is the transport of polarizable Mycobacteria additionally possess a pseudocapsule of noncova- particles in response to a nonuniform electric field, lently attached lipids. Mycolic acids, specifically the complex exclusive of electrophoresis.1 DEP forces depend on the trehalose dimycolate in M. tuberculosis, are responsible for the magnitude and nonuniformity of an externally applied electric host inflammatory and granulomatous responses4,5 that are the field, as well as the complex permittivity of a particle and its primary symptoms of tuberculosis infection. In addition to their surrounding media.2 The complex permittivities of the particle adjuvant effects on the host immune system, the lipid content of and surrounding media are a function of the frequency of the mycobacterial species forms a dense, hydrophobic barrier to polarizing electric field, electrical conductivity, and permittiv- antibiotics, contributing to mycobacterial drug resistance.
ity. Material permittivity values constitute an instantaneous These membrane lipids are bound to the polysaccharide approximation of the medium response and are, thus, generally arabinogalactan.6 The antimycobacterial drug ethambutol inhi- a function of the electric field frequency, depending on the bits biosynthesis of arabinogalactan, limiting mycolate attach- orientational, atomic, and electronic polarizabilities.3 Over the ment sites and significantly altering membrane composition.7 range of frequencies considered in this work, however, these Due to its role in pathogenicity and host immune response, the effects are negligible and the permittivity, ε, is assumed exterior lipid composition of the cell membrane of mycobacterial independent of frequency. The combination of material and species is relevant to studies of membrane biosynthesis, drug frequency dependence makes DEP a useful technique for resistance, and pathogenicity.
researchers attempting to manipulate, separate, and character- DEP devices have been used to characterize and separate a ize particles and cells.
variety of species, e.g., bacterial populations,8
11 mammalian In this work, we present an automated DEP-based character- cells,12
15 DNA,16 proteins,17
20 and viruses.21 Indeed, DEP ization technique and apply it to the bacterial species Mycobac- devices have been used to identify surface monolayer and terium smegmatis. M. smegmatis is a nonpathenogenic, acid-fast, membrane properties of particles and cells, respectively.22,23 Gram-positive bacteria with a membrane structure similar toother, pathogenic species such as M. tuberculosis. The outer layer of M. smegmatis is composed of covalently attached lipids, namely R-, keto-, and methoxy-mycolic acids. Some Published: April 04, 2011 r 2011 American Chemical Society dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515

Analytical Chemistry solution can be found2,27 for particles oriented with their longaxis parallel to the external electric field (along the z axis): DEP, zæ ¼ πεmlzlx, y R 3½ εm þ ð εp
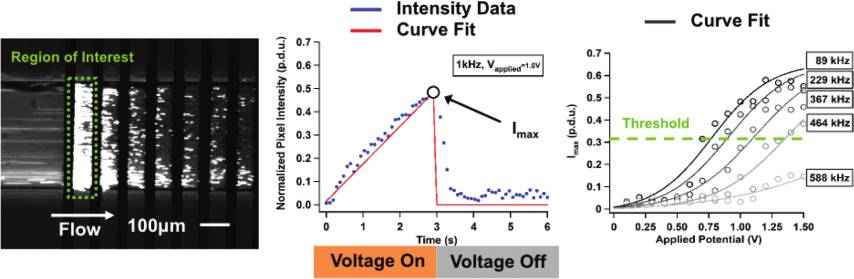
εmÞLz where lz and lx (= ly) are the lengths of the major and minor axes,respectively. Lz is the "depolarizing factor" along the major axis: Figure 1. Interdigitated electrode array configured with alternating positive (Vþ) and negative (V
) electrodes on the bottom of a microfluidic channel. Fluid drag moves particles with the direction of flow while pDEP forces attract particles to the electrode array. Negative x,y /lz )1/2 is the particle eccentricity.
DEP forces repel particles from the array.
To describe particles with inhomogeneous complex permit- tivity such as cells, a multishell model is often invoked, usingspherically symmetric layers of constant thickness, permittivity, DEP separation techniques are often binary, centering on the and conductivity.28
30 Using the same change of variables, an crossover frequency, at which the sign of the DEP force changes.
ellipsoidal particle can also be described with the multishell For samples with different crossover frequencies, there exists a approach, if the shells can be approximated as confocal. Although frequency regime where the DEP force is positive for one this is typically not exact for cells, the ellipsoidal multishell model population and negative for another. Another class of DEP-based provides a convenient analytical tool to describe coccoidal separation techniques depend on differences in the magnitude of bacteria. A prolate spheroid with a single shell of complex the DEP force at a particular frequency.8,11,24,25 Because the permittivity, ε S, has a dipole coefficient (analogous to fCM for crossover frequency can be insensitive to changes in cell mem- spherical particles): brane composition (the primary component affected byethambutol), it is beneficial to investigate separation techniquesthat depend on the magnitude of the DEP force. These separa- tion techniques require characterization of cellular dielectric 3½ εm þ L1ð εs
εmÞ þ 9 response as a function of frequency to determine the optimal regime for efficient operation.
where γ is the ratio of volumes of the core to the whole spheroidand Kz,0 is the spheroidal complex Clausius
Mossotti factor: We use a combination of numerical and analytical techniques 3½ εs þ L1ð εp
εsÞ to model particle behavior near an interdigitated electrode array.
The configuration of the array and the direction of positive DEP Additional shells can be added as described by Castellarnau forces are shown in Figure 1.
et al.11 and Huang et al.,31 with the n-shell factor described Dielectrophoresis and Cell Modeling. We start by consider- ing a sphere in an infinite domain with homogeneous and isotropic complex permittivities. In a uniform field E = E0 cos(ωt), the contribution of a polarized sphere to the total εn
1 þ Lz,nð εm
εn
1ÞÞ electric field can be described by an electric dipole with a moment,2,3,26 p = p0(cos ωt þ j): ðhlx,y þ ∑ δkÞðlx,y þ ∑ δkÞ2 where a is the particle radius, E is the externally applied ðhlx,y þ ∑n δkÞðlx,y þ ∑n δkÞ2 electric field, and the subscripts m and p refer to the medium and particle, respectively. ε = ε
iσ/ω is the complex permittivity, is the permittivity, σ is the electrical conductivity, ω is the frequency of the applied electric field (in rad/s), and i = (
1)1/2. If the field is slightly nonuniform over the length scale of the particle, then the force on the dipole will be F = p 3 rE. Assuming no net free charge, this yields the following expression for the time-averaged dielectrophoretic force:2 ÆF CM)r(E0 3 E0).
For ellipsoidal particles (specifically, a prolate spheroid), a hlx, y þ ∑n δk change of variables can be performed, and a similar analytical dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515

Analytical Chemistry between trials and samples. This trapping potential data isinversely proportional to the square root of R [ fCM] and allowsfor the relative magnitudes of the particles' DEP responses to bemeasured.
The electric field above a pair of interdigitated electrodes can be approximated by assuming that the gap between the electro-des is differentially small. The resulting expressions for theelectric field and the dielectrophoretic force on a homogeneousspherical particle are8,36 Figure 2. Interdigitated electrode array schematic with regions ofinterest (ROI-1 and ROI-2) defined. The average pixel intensity inROI-1 was used as a background intensity signal proportional to particle ÆFDEPæ ¼ a3εmR ½ f V2 r density and fluorescence staining intensity. The average pixel intensity in ROI-2 was used as a measure of particle trapping. Inset shows a top view where θ and r are unit vectors in cylindrical coordinates, r is the of the fabricated device with PDMS channel.
radial distance from the center of the electrode gap, and V is theapplied potential.
where h = lz/lx,y is the particle spheroid aspect ratio (h > 1 for a Following the analysis of Sanchis et al.,8 we assume that prolate spheroid) and δn refers to the thickness of the nth shell. In particles reach terminal velocity instantaneously and that particle an effort to account for some of the error induced by the confocal trapping occurs in a stagnant fluid. Under these conditions, we shell approximation, specifically that incurred due to varying shell can calculate the time required to trap a particle on the electrode thicknesses, eqs 7 and 9 redefine the volume ratio, xn, and array from a distance rtrap from the electrode gap. The resulting eccentricity, en, to exclude the aspect ratio, h, from the shell relationship gives the approximate number of cells, N, on the thickness parameter, δn.
array after a time, Δt, given a cell number density, n0. rtrap defines In this study, a three-shell model (n = 5) was used to a trapping horizon that expands as Δt increases. During the time, approximate the structure and composition of bacterial samples.
Δt, N cells within a semicylindrical volume swept by rtrap are This model accounts for the complex permittivity and relative trapped on the array.
sizes of the cytoplasm (n = 1), cytoplasmic membrane (n = 2), cell wall (n = 3), and media (n = 5). The outer shell (n = 4) of the particle was used to approximate the outer membrane in E. coli samples and the covalently bound lipids in M. smegmatis samples.
The homogeneous sphere model for polystyrene in water where w is the channel width (length of electrode) and η is the neglects the significant surface conductance that dominates the fluid viscosity. The addition of a pressure-driven (Poiseuille) flow particle response at low frequency. It has been shown by several profile will transform (scale and shear) the trapping horizon but researchers that carboxylate-modified polystyrene microspheres is not expected to significantly alter the scaling relationship exhibit a significant surface conductance that contributes to between N and the applied potential, V. We can rearrange this particle dielectrophoretic behavior.33
35,40,41 Polystyrene micro- relationship to express fCM as a function of the trapping spheres are therefore modeled as a homogeneous particle with a potential, Vtrapping: surface conductance that contributes significantly to the effectiveparticle conductivity:32
35 0 w2a2εm Δt Vtrapping p ¼ σp, bulk þ 2 The number density and trapping time, Δt, are fixed parametersin the experiment, so the number of cells collected is a function of p,bulk is the bulk particle conductivity and Ks is the surface [ fCM]. Rather than measuring the number of captured cells, as done in other DEP collection experiments,8,14 we measure the Electric Field and Cell Collection Modeling. The DEP force potential, Vtrapping, required to trap a particular number (or, more is a direct function of the electrical properties of the particle and precisely, number density) of cells in a region of interest. Vtrapping the fluid medium (related by the real part of the Clau- is defined by a threshold value of the maximum fluorescence sius
Mossotti factor, R [ fCM]), as well as the magnitude and intensity, Imax, discussed in the next section. By defining Vtrapping frequency of the applied electric field. To characterize the DEP as the potential where the measured fluorescence intensity is response of particles and cells, we fabricated a device with a Imax/2, we account for experiment-to-experiment variations in microchannel defined in poly(dimethylsiloxane) (PDMS) and bonded on top of gold interdigitated electrodes deposited on Data Collection and Analysis. Here we describe the theore- glass (Figure 2, inset). In certain ranges of electric field magni- tical aspects of our data collection and analysis procedure, tude and frequency, the positive DEP force acting on a particle specifically the definition of Vtrapping and Imax in terms of will overcome fluid drag and trap the particle onto the electrodes.
experimental data. An automated data collection scheme was The intensity of trapped, fluorescently labeled particles was developed to measure particle trapping as a function of electric recorded over time and was fit to a series of physically informed field frequency and magnitude (electric field parameters vary and functions such that a quantitative measure of particle trapping, a are discussed later in Materials and Methods). A custom LabVIEW "threshold trapping potential", can be defined and compared interface controlled the electric field inputs of the experiment— dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515

Analytical Chemistry accounts for permanent particle adhesion over the course of theexperiment. Next, "on-time" data from each experimental condi-tion was fit to a quadratic curve which served as a low-pass filterfor measurement noise (Figure 3). The "on-time" and "off-time"analyses were performed over all experimental conditions withineach data subset (i.e., for each frequency), and the maximumquadratic fit for the entire experiment (i.e., over all potentials andfrequencies) was recorded as Imax. Finally, for each data subset, thepeaks of the quadratic curves were fit to a sigmoidal curve with apeak plateau region set to Imax.
Identifying a unique value of I Figure 3. Raw average pixel intensity data from ROI-2 (blue points) max for each (experimental) data was fit to quadratic curves (solid red) at each "experiment condition"— set corrected for experimental variability due to particle concen- corresponding to a particular frequency
potential pair. In this example tration variations or electrode surface contamination between data set, taken at 1 kHz with polystyrene beads, experimental conditions experiments. A sigmoidal fit was chosen because it characterizes 1
15 correspond to applied potentials of 0.1
1.5 V in 0.1 V increments.
the trapping behavior of particles well, including a lower region The peaks of each quadratic fit were fit to a sigmoid (dashed black) before trapping is observed and a saturation region as the trapped whose plateau was determined by the maximum measured average pixel particles fill the space near the electrodes. If the goodness of the intensity for all frequency
potential pairs in an experiment.
sigmoidal fit did not exceed a defined threshold (R2 > 0.7), thenthe data subset from that particular applied frequency was magnitude, frequency, "on" duration, and "off" duration— excluded. In almost all cases, data subsets for which R2 < 0.7 and recorded the fluorescence intensity outputs. Fluorescence occurred at frequencies where ÆF is expected to be low or intensity was integrated over a region of interest and normalized by negative and no particles trapped in the region of interest.
the number of pixels to give an average pixel intensity. The average The threshold trapping potential, Vtrapping, for each applied pixel intensity is then a function of the magnitude of the DEP force, frequency was defined as the voltage at which the sigmoidal fit which in turn depends on particle composition and on electric field function at that frequency has a value of Imax/2; for frequencies at magnitude and frequency. Inflow particle density was assumed which DEP forces are weak, this gives values larger than the uniform and constant throughout all experiments. Variations in experimental voltage range, with increased uncertainty asso- particle fluorescence intensity were controlled by careful staining ciated with the extrapolation of the data. The trapping potential protocols and corrected for during data analysis by comparing as a function of frequency was obtained for polystyrene particles trapping data to bulk sample concentration.
or bacteria in solutions of varying conductivity. The inverse The spatially averaged pixel intensity was recorded over the square of the trapping potential was calculated to compare the course of the experiment for two separate regions of interest: relative DEP response magnitudes of the particles and cells.
upstream of the electrode array (ROI-1) and around the gapsbetween the first, second, and third electrodes (ROI-2, Figure 2).
' MATERIALS AND METHODS ROI-1 was used as a representative measure of bulk sampleconcentration to account for changes in particle number density.
Device Fabrication. Electrodes were fabricated by use of ROI-2 measured the intensity of particles trapped on the array.
standard lift-off photolithography. Four inch borofloat glass The order in which frequencies were applied was randomized for wafers were cleaned with hot piranha solution and vapor-primed every experiment. Three experiments were performed for every with HMDS. Microposit S1818 photoresist was spun onto the trial, and for biological samples, each trial was a separately wafers at 3000 rpm for 30 s and baked at 115 C for 60 s.
cultured and prepared sample.
Photoresist was exposed with an EV620 contact aligner in soft- To quantitatively compare sample DEP response, a series of contact mode for 2 s (12 mW/cm2). Photoresist was developed analyses were performed in MATLAB to account for background in Microposit MF-321 for 120 s. Wafers were then treated for 90 s fluorescence, particle density fluctuations, and permanent particle with oxygen plasma to descum and then placed in a CVC SC4500 adhesion to the electrodes. Data from each experiment was electron-beam evaporator. A 200 nm layer of gold was deposited broken down into subsets containing data for a particular between 50 nm and 10 nm layers of chrome. Lift-off was frequency. Within each frequency subset, we identify "experiment performed in a Microposit Remover 1165 for 12 h. Wafers were conditions" corresponding to a particular frequency
potential then coated with resist and diced (K&S 7100 dicing saw).
pair. Data for each experiment condition is a time series of Fluid channel fabrication was accomplished by use of standard normalized pixel intensity data within each ROI with the electric soft lithography. First, a silicon master was fabricated with 25 μm field on then off. To account for variations in particle solution tall features by use of standard photolithography. Wafers were concentration, the bulk particle concentration signal (ROI-1) was coated with Microposit S1818 photoresist (3000 rpm, 30 s) and subtracted from the particle trapping signal (ROI-2) for the entire exposed for 2 s (12 mW/cm2). Features were etched to a depth of experimental data set. Next, "off-time" data from each experi- 25 μm with a Unaxis 770 Bosch reactive ion etch tool and resist- mental condition was smoothed by a locally weighted scatterplot stripped with reactive oxygen plasma (Gasonics Aura 1000).
smoothing function, and the minimum of this smoothed curve Wafers were coated with 1H,1H,2H,2H-perfluorooctyltrichloro- was subtracted from the experiment condition data; this step silane (FOTS) by use of a vacuum evaporation process to prevent dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515 Analytical Chemistry PDMS adhesion. PDMS monomer and curing agent were mixed Beads were spun down at 5000g for 10 min and resuspended in in a 15:1 ratio for 5 min and placed under vacuum to remove DI water with trace amounts of salt (KCl) to control conductiv- bubbles. The PDMS mixture was then poured over the silicon ity. Particles were diluted to a density of ∼4.25  106 particles/ master in a custom-made jig and placed in an oven to cure for 12 h mL in polystyrene bead samples.
at 60 C. PDMS devices were cut to size, and via holes were Data Acquisition and Processing. Prepared samples were created with a biopsy punch. PDMS channels and electrode drawn into a Hamilton Gastight 1000 1 mL glass syringe devices were cleaned in an air plasma at 250 mTorr vacuum for (Hamilton Company, U.S.A.) and dispensed at a rate of 10 45 s (Harrick Plasma) and immediately bonded. Electrodes were μL/h by a Chemyx Fusion 400 syringe pump. The precision glass connected externally to wires with silver conductive epoxy.
syringe and high step resolution of the syringe pump (0.02 μm) Sample Preparation. Lyophilized E. coli (K-12 wild-type, combined to significantly reduce variability in the volumetric EMG 2: K (lambda), ATCC 23716, passage 1
2) and M.
flow rate. The syringe was coupled to the PDMS channel with a smegmatis (mc(2)155, ATCC 700084, passage 1
2) samples 30 gauge needle and Tygon microbore tubing (o.d., 0.76 mm; were obtained from ATCC. Cultures were grown in LB media i.d., 0.25 mm). Electric potentials were applied to the electrode (E. coli) and Middlebrook 7H9 media with OADC enrichment array by an Agilent 33200A arbitrary waveform generator and (100 mL/L) (M. smegmatis), respectively. Media solutions were controlled with a custom LabVIEW interface (National Instru- obtained from Becton/Dickinson and prepared as directed by ments Corporation, U.S.A.).
the manufacturer, with the exception of using OADC enrichment The LabVIEW interface controlled the electric field frequency, in Middlebrook 7H9 media. E. coli cells were grown in liquid magnitude, "on" time, and "off" time. The "on" time was fixed at 3 media (10 mL of LB broth) in an incubating shaker at 37 C and s for all experiments, and the "off" time was 3 s for polystyrene 350 rpm for 24 h. E. coli were then plated in Petri dishes on LB bead samples and 5 s for biological samples. Electric field agar (prepared as directed by the manufacturer) and incubated frequencies (40 points, logarithmically spaced between 1 kHz for 24 h at 37 C. M. smegmatis cells were grown under the same and 10 MHz) were ordered randomly in each experiment and conditions in liquid media (10 mL of Middlebrook 7H9) for 48 h.
tested at every potential. Potentials were applied, in order, from M. smegmatis cells were then plated on LB agar with 0.5 mL/L 0.1 to 1.5 V in 0.1 V increments (2.5 V in 0.2 V increments in Tween 80 and incubated for 48 h at 37 C. Petri dishes were then ethambutol-treated M. smegmatis experiments) to minimize sealed with paraffin, inverted, and refrigerated.
electrode fouling over the course of the experiment.
E. coli cells were taken from first or second passage solid Particle trapping was measured with a Nikon LV100 upright culture and placed in 10 mL of LB media in sterile 14 mL microscope with long working distance objectives (Nikon S Plan polystyrene culture tubes (loosely capped). Samples were al- Fluor, 40/0.60, 3.6
2.8 mm), a EXFO X-Cite series 120 lowed to grow through log phase to stationary phase (18
24 h) fluorescence excitation source, and a QImaging EXiFast Blue before preparation. M. smegmatis samples were prepared identi- high-speed monochrome CCD camera.
cally with the exception of culture media (Middlebrook 7H9 with Safety. Electrical components present a shock hazard. Dis- OADC enrichment) and growth time to stationary phase connect electrical power while making connections and take (36
48 h). Cells were grown to stationary phase—as deter- proper safety precautions when energizing electrical compo- mined by representative growth rate experiments, optical density nents. Biological specimens and toxic chemicals (e.g., (OD650) measurements (data not shown), and data available in ethambutol) should be handled with care. Appropriate personal literature37—prior to preparation. To assess the impact of cell protective equipment should be worn at all times and disposed of membrane composition on DEP response, samples of M. smeg- matis were treated with ethambutol (ETB) at a concentration of10 μg/mL after 24 h of growth, and the treatment was main- ' RESULTS AND DISCUSSION tained at this concentration throughout preparation and experi-ment. 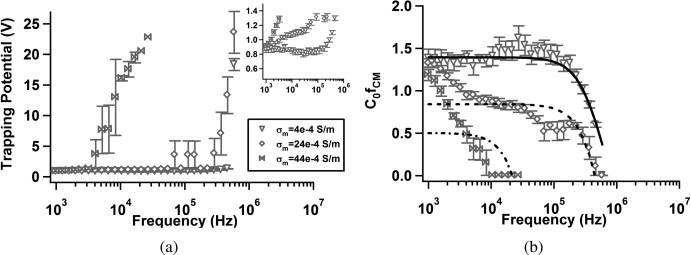Growth in liquid culture was carried out in an incubating Polystyrene Microspheres. Carboxylate-modified polystyr- shaker at 37 C at 350 rpm. Samples of 1 mL were removed and ene microspheres were tested in solutions with three different placed in centrifuge tubes and spun down at 5000g for 10 min.
conductivities (adjusted by addition of KCl) to show that, as The samples were resuspended in 0.85% (w/v) NaCl in deio- expected, trapping potential increases in the low-frequency nized water and allowed to incubate for 1 h. Samples were then regime as media conductivity increases. This is consistent with spun down again and resuspended in 0.85% (w/v) NaCl with 4 a decrease in R [ fCM] over the same frequency range. The μL/mL of BACLight live/dead stain (Molecular Probes) and apparent crossover frequency is ∼106 Hz, decreasing with allowed to incubate in the dark (culture oven, 37 C) for 1 h. The increasing conductivity in Figure 4, parts a and b.
samples were then washed once with and then resuspended in The data in Figure 4b were fit to eq 10 by use of a nonlinear 0.5% (w/v) Tween 80 solution (a subset of E. coli samples were least-squares method in MATLAB. Fits shown in Figure 4b were processed in DI water for comparison). M. smegmatis samples were calculated using the constants listed in Table 1 with C0 and Ks as analyzed to confirm that treatment with ethambutol did not free parameters. C0 is a scaling constant related to flow conditions meaningfully affect fluorescence intensity or cell size. A represen- and electrode geometry. Fixed parameter values were set to exact tative sample was evaluated with Phylum analysis software for cell values, whereas free parameters were constrained to physically length and diameter as well as average intensity. Wild-type and reasonable values inferred from previously published data.33
35,41 ethambutol-treated samples exhibited lengths of 1.24 and 1.33 μm Low-conductivity data was well-fit by a simple surface conductivity with standard deviations of 0.14 and 0.11 μm, respectively. Average model (eq 10) with the parameters listed in Table 1. However, as pixel intensity per cell was 1037 p.d.u. (WT) and 1041 p.d.u (ETB) conductivity increased, the model becomes less appropriate, as with standard deviations of 49.9 and 45.1, respectively.
evidenced by decreasing values of R2. The values obtained for Fluoresbrite 1.75 μm diameter carboxylate-modified polystyr- surface conductance are similar to those proposed by Green and ene microspheres (beads) were obtained from Polysciences, Inc.
Morgan33 and Hughes and Morgan.35 The crossover frequency dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515

Analytical Chemistry Figure 4. Trapping potential, V trapping, (a) and C0 [ fCM](= 1/Vtrapping ) (b) as a function of frequency for 1.75 μm diameter carboxylate-modified polystyrene particles suspended in aqueous solutions with conductivities σm = 4  10
4, σm = 24  10
4, and σm = 44  10
4. Inset in panel a expandsthe low-potential range for clarity. Inset axes are the same as panel a: Vtrapping (ordinate) and frequency (abscissa). Curve fits in panel b were calculatedwith an effective surface conductance model (eq 10). Error bars represent standard error of the mean: Se = Sd/(n)1/2 where Sd is the standard deviation.
The symbol C0 denotes an arbitrary constant related to the flow rate and electrode geometry.
Table 1. Multivariable Fit Coefficients Chosen to MatchExperimental Measurements of the Real Part of the Clau-sius
Mossotti Factor, R [ fCM], for Carboxylate-Modified a Polystyrene Particles in Solutions of Increasing Conductivity Figure 5. C R [ f 2) as a function of frequency for CM](= 1/Vtrapping wild-type E. coli suspended in DI water (filled circles, σ ≈ and 0.5% (w/v) Tween 80 solution (open circles, σ ≈ 1 mS/m). Curve Parameters are divided into fixed (above) and free (below) groups.
fits for E. coli in DI water (solid) and 0.5% (w/v) Tween 80 solution Fixed parameters and limits of free parameters were based on previously (dashed) were calculated using a multivariate nonlinear least-squares published data (refs 33
35, 41).
technique to a spheroidal multishell model. Error bars representstandard error of the mean. The symbol C0 denotes an arbitrary constant predicted by a homogeneous-particle model remains constant at related to the flow rate and electrode geometry.
low medium conductivity (<∼1  10
3), then decreases rapidlyand disappears when ε m > ε p.33 The experimentally observed (w/v) Tween 80 were fit as before, allowing the permittivity of decrease in crossover frequency with increasing conductivity is the outer membrane to vary. The results of fitting are given in often attributed to surface conductance and double layer polariza- Table 2. In the presence of 0.5% (w/v) Tween, the outer tion effects.33 Recent work by Basuray and co-workers has membrane permittivity increased by a factor of 3. Although by managed to capture this change in crossover frequency by con- no means conclusive, this result suggests that the presence of the sidering polarization and ion transport within the double layer.38,39 surfactant in solution may have interacted with the outer E. coli. As additional verification of our experimental data membrane and contributed to the local effective permittivity.
collection and data analysis techniques, we measured the pDEP M. smegmatis. M. smegmatis is a Gram-positive bacterium response of E. coli in DI water and 0.5% (w/v) Tween 80 with both a different shape and different composition from E. coli.
solution. The results, Figure 5, show a constant trapping poten- We therefore expect a different trapping response owing to the tial for low frequency which then increases above 105 Hz and presence of the lipid/mycolic acid region of the mycobacterial peaks near 106 Hz before decreasing again. This is consistent with envelope. Indeed, we do observe such a distinction, particularly our model predictions for E. coli as well as experimental results below ∼106 Hz where E. coli samples exhibit significant low- obtained by Sanchis et al.8 and Castellarnau et al.11 frequency dispersion that is not observed in M. smegmatis.
The data were well-fit by the spheroidal three-shell model This low-frequency component to the DEP response is indica- discussed previously (i.e., eq 6). To obtain these fits, two rounds tive of multiple Maxwell
Wagner relaxation frequencies, of fitting were performed. Initial fits for E. coli in DI water were which can result when the interfaces between materials are performed, allowing all parameters to vary while constrained by not well-defined. At still lower frequencies (i.e., 1  104 Hz) values obtained in the literature.8,11 After initial fitting, cytoplas- the so-called R-relaxation associated with ion motion within the mic, plasma membrane, and cell wall coefficients were fixed along double layer is one potential explanation for the observed pDEP with outer membrane conductivity, and data for E. coli in 0.5% dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515

Analytical Chemistry Table 2. Multivariable Fit Coefficients for the Clau- Table 3. Multivariable Fit Coefficients for the Clau- sius
Mossotti Factor, R [ z], for E. coli in Deionized Water
Mossotti Factor, R [ Kz], for Wild-Type and Ethambu- and a 0.5% (w/v) Solution of Tween 80 (Figure 5) tol-Treated M. smegmatis in a 0.5% (w/v) Solution of Tween 0.5% (w/v) Tween 80 ETB-treated M. smegmatis Parameters are divided into fixed (above) and free (below) groups.
Fixed parameters and limits of free parameters were based on previously Parameters are divided into fixed (above) and free (below) groups.
published data (refs 8 and 11).
Fixed parameters and limits for free parameters were based on previouslypublished data (refs 8, 11, 47
50).
and shifted toward higher frequencies (∼106
107 Hz). Thedramatic difference observed in Figure 6 confirms the effect thatethambutol has on mycobacterial membrane composition. Thedata in Figure 6 can be fit by the spheroidal multishell modelintroduced earlier. Parameters used to generate curve fits aregiven in Table 3. The aspect ratio, h, for M. smegmatis was 3.3,calculated from measurements by Nguyen et al.46 Thicknesseswere estimated based on the work of Takade et al.47 and Paul andBeveridge48
50 or inferred from the curve fit process.
The results of the curve fitting analysis indicate a wide range of changes within the cell membrane as a result of treatmentwith ethambutol. There are slight variations in the permittivityand conductivity of the plasma membrane and cell wall, and anincrease in cytoplasmic conductivity. The most dramatic [ fCM](= 1/Vtrapping ) as a function of frequency for change, however, occurs in the outer membrane or lipid region, wild-type (open squares) and ethambutol-treated (open triangles) M.
where both the permittivity and conductivity increased to smegmatis suspended in 0.5% (w/v) Tween 80 solution (σ ≈ approximately those of the external media. The thickness of Curve fits for wild-type (solid) and ethambutol-treated (dashed) the lipid region also decreased. These are both suggestive of the samples were calculated using a multivariate nonlinear least-squares antimycolic acid action of ethambutol, which has been shown technique to a spheroidal multishell model. Error bars representstandard error of the mean. The symbol C to prevent the attachment of mycolic acids in the outer 0 denotes an arbitrary constant related to the flow rate and electrode geometry.
Chan et al. examined the accuracy and sensitivity of para- meters extracted from electrorotation data (related to DEP Treatment with ethambutol significantly alters the dielectro- trapping data by Kramers
Kr€onig relationships) by use of a phoretic response of M. smegmatis. Mycobacteria are susceptible three-shell model.51 Their results indicate that the accuracy of to modification of their membrane composition using ethambu- extracted inner membrane and cytoplasmic parameters de- tol to inhibit the production of arabinogalactan and prevent the creased as noise in the electrorotation data increased. This attachment of mycolic acids. The removal of the outer layer of indicates that the effects of these material properties are some- lipids exposes the peptidoglycan6,45 and significantly decreases what subtle and difficult to extract relative to parameters such as the effective permittivity of the cell. Treatment with ethambutol the outer membrane permittivity. In our analysis, we noticed caused the values of 1/V to be significantly diminished qualitatively similar behavior when we used unconstrained dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515 Analytical Chemistry parameters; large variations in inner membrane parameters elicited subtle changes, while outer-shell parameters affected This work is supported by the National Science Foundation, gross changes in the resulting fit. As a result, the data obtained Grant CBET-0828997. B.G.H. and C.H. also acknowledge in this work reflects changes in a lumped, membrane capacitance support from NSF Graduate Research Fellowships.
parameter. In an attempt to correlate these results with physicalchanges in cell structure, we refine the lumped parameter modelinto multiple components (shells). In doing so, we sacrifice the uniqueness of our results but demonstrate consistency with the (1) Pohl, H. A. Dielectrophoresis: The Behavior of Neutral Matter in proposed changes in membrane structure. The key conclusions Nonuniform Electric Fields; Cambridge University Press: New York, of this work are that the changes measured in E. coli and M.
smegmatis are consistent with, and suggestive of, changes in the (2) Jones, T. B. Electromechanics of Particles; Cambridge University outer membrane structure.
Press: New York, 1995.
A wide array of techniques are available for characterization of (3) Morgan, H.; Green, N. G. AC Electrokinetics: Colloids and the dielectrophoretic response of a sample. The majority rely on Nanoparticles; Research Studies Press: Hertfordshire. U.K., 2003.
electrorotation12,31,52
54 or measurements of the crossover (4) Rhoades, E. R.; Geisel, R. E.; Butcher, B. A.; McDonough, S.; frequency.11 The electrorotation force is largest at the crossover Russell, D. G. Tuberculosis (Edinburgh, Scotland) 2005, 85, 159–176.
frequency, making measurements in this frequency regime easier, (5) Korf, J.; Stoltz, A.; Verschoor, J.; De Baetselier, P.; Grooten, J.
Eur. J. Immunol. 2005, 35, 890–900.
compared to the positive and negative DEP forces, which are (6) Alsteens, D.; Verbelen, C.; Dague, E.; Raze, D.; Baulard, A. R.; vanishingly small approaching the crossover frequency and tend to Dufr ene, Y. F. Pfluegers Arch: Eur. J. Physiol. 2008, 456, 117–125.
be larger, and thus easier to measure, far from the crossover (7) Mikusova, K.; Slayden, R. A.; Besra, G. S.; Brennan, P. J.
frequency.51,55 The use of DEP "collection spectra" has been Antimicrob. Agents Chemother. 1995, 39, 2484–2489.
employed to characterize a number of different cell types, to screen (8) Sanchis, A.; Brown, A. P.; Sancho, M.; Martnez, G.; Sebastian, bacteria for antibiotic resistance, and to detect cancerous J. L.; Mu noz, S.; Miranda, J. M. Bioelectromagnetics 2007, 28, 393–401.
cells.8,14,56,57 By associating fluorescence intensity with collection (9) Lapizco-Encinas, B. H.; Simmons, B. A.; Cummings, E. B.; spectra, we can automate the data collection and analysis process.
Fintschenko, Y. Anal. Chem. 2004, 76, 1571–1579.
The resulting quantitative characterization of V (10) Cho, Y.-K.; Kim, S.; Lee, K.; Park, C.; Lee, J.-G.; Ko, C.
trapping allows com- parison of the magnitude of pDEP forces on a particular sample, a Electrophoresis 2009, 30, 3153–3159.
(11) Castellarnau, M.; Errachid, A.; Madrid, C.; Juarez, A.; Samitier, crucial step when developing dielectrophoresis-based sorting tech- J. Biophys. J. 2006, 91, 3937–3945.
niques that rely on a difference in the magnitude of R [ fCM].
(12) Yang, J.; Huang, Y.; Wang, X.; Wang, X.-B.; Becker, F. F.; Gascoyne, P. R. C. Biophys. J. 1999, 76, 3307–3314.
(13) Yang, J. Biophys. J. 2000, 78, 2680–2689.
(14) Gascoyne, P.; Noshari, J.; Becker, F.; Pethig, R. IEEE Trans. Ind.
In this work, we present a novel automated experimental tech- Appl. 1994, 30, 829–834.
(15) Das, C. M.; Becker, F.; Vernon, S.; Noshari, J.; Joyce, C.; nique with which we measured the effects of ethambutol treat- Gascoyne, P. R. C. Anal. Chem. 2005, 77, 2708–2719.
ment on the positive dielectrophoretic response of M. smegmatis.
(16) Chou, C. F.; Tegenfeldt, J. O.; Bakajin, O.; Chan, S. S.; Cox, This represents the first such characterization of the dielectro- E. C.; Darnton, N.; Duke, T.; Austin, R. H. Biophys. J. 2002, phoretic response of M. smegmatis. In addition, experiments 83, 2170–2179.
were performed to measure the pDEP response of carboxylate- (17) Clarke, R. W.; White, S. S.; Zhou, D.; Ying, L.; Klenerman, D.
modified polystyrene microspheres and wild-type E. coli. Poly- Angew. Chem., Int. Ed. 2005, 44, 3747–3750.
styrene bead data were fit with a surface conductance model, (18) Clarke, R.; Piper, J.; Ying, L.; Klenerman, D. Phys. Rev. Lett.
and bacterial data were fit with a spheroidal multishell model.
2007, 98, 198102–6.
The results of this characterization technique garner insight (19) H€olzel, R.; Calander, N.; Chiragwandi, Z.; Willander, M.; Bier, into frequency regimes where membrane-specific differences F. Phys. Rev. Lett. 2005, 95, 128102–4.
(20) Lapizco-Encinas, B. H.; Ozuna-Chacon, S.; Rito-Palomares, M.
in mycobacterial cells manifest as significant changes in their J. Chromatogr., A 2008, 1206, 45–51.
(21) Hughes, M.; Morgan, H.; Rixon, F.; Burt, J.; Pethig, R. Biochim.
The automated pDEP characterization of wild-type and Biophys. Acta 1998, 1425, 119–126.
ethambutol-treated M. smegmatis performed in this study shows (22) Vykoukal, J.; Vykoukal, D. M.; Sharma, S.; Becker, F. F.; that ethambutol significantly alters cell dielectrophoretic re- Gascoyne, P. R. C. Langmuir 2003, 19, 2425–2433.
sponse in a manner that is consistent with a removal or (23) Oblak, J.; Krizaj, D.; Amon, S.; Macek-Lebar, A.; Miklavcic, D.
permeabilization of the outer lipid structure of these cells.
Bioelectrochemistry 2007, 71, 164–171.
Wild-type (mc(2)155) M. smegmatis exhibit pDEP response (24) Das, C. M.; Becker, F.; Vernon, S.; Noshari, J.; Joyce, C.; above 5  104 Hz, whereas ethambutol-treated bacteria exhibited Gascoyne, P. R. C. Anal. Chem. 2005, 77, 2708–2719.
pDEP response only above 2  107 Hz. This frequency regime (25) Hawkins, B. G.; Smith, A. E.; Syed, Y. A.; Kirby, B. J. Anal. Chem.
2007, 79, 7291–7300.
may represent a key frequency space where dielectrophoresis- (26) Kirby, B. J. Micro- and Nanoscale Fluid Mechanics: Transport in based sorting techniques can be implemented to measure Microfluidic Devices; Cambridge University Press: New York, 2010.
changes in mycobacterial membrane properties associated with (27) Stratton, J. A. Electromagnetic Theory; McGraw-Hill: New York, chemical treatments or genetic mutation.
(28) Hughes, M. P.; Morgan, H.; Rixon, F. J.; Burt, J. P.; Pethig, R.
' AUTHOR INFORMATION Biochim. Biophys. Acta 1998, 1425, 119–126.
(29) Froude, V. E.; Zhu, Y. J. Phys. Chem. B 2009, 113, 1552–1558.
Corresponding Author (30) Korlach, J.; Reichle, C.; M€uller, T.; Schnelle, T.; Webb, W. W.
Biophys. J. 2005, 89, 554–562.
dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515 Analytical Chemistry (31) Huang, J. P.; Gu, G. Q.; Karttunen, M. Phys. Rev. E 2003, (32) Bikerman, J. J. Trans. Faraday Soc. 1940, 35, 154.
(33) Green, N. G.; Morgan, H. J. Phys. Chem. B 1999, 103, 41–50.
(34) Hughes, M.; Morgan, H.; Flynn, M. J. Colloid Interface Sci. 1999, 220, 454–457.
(35) Hughes, M. P.; Green, N. G. J. Colloid Interface Sci. 2002, 250, 266–268.
(36) Ramos, A.; Morgan, H.; Castellanos, A. J. Phys. D: Appl. Phys.
1998, 31, 2338–2353.
(37) Tran, S. L.; Cook, G. M. J. Bacteriol. 2005, 187, 5023–5028.
(38) Basuray, S.; Chang, H.-C. Phys. Rev. E 2007, 75, 2–5.
(39) Basuray, S.; Wei, H.-H.; Chang, H.-C. Biomicrofluidics 2010, (40) Arnold, W. M.; Schwan, H. P.; Zimmermann, U. J. Phys. Chem.
1987, 91, 5093–5098.
(41) Hughes, M.; Morgan, H.; Flynn, M. J. Colloid Interface Sci. 1999, 220, 454–457.
(42) Lyklema, J.; Dukhin, S.; Shilov, V. J. Electroanal. Chem. 1983, 143, 1–21.
(43) Springer, M.; Korteweg, A.; Lyklema, J. J. Electroanal. Chem.
1983, 153, 55–66.
(44) Lyklema, J.; Springer, M.; Shilov, V.; Dukhin, S. J. Electroanal.
Chem. 1986, 198, 19–26.
(45) Verbelen, C.; Dupres, V.; Menozzi, F. D.; Raze, D.; Baulard, A. R.; Hols, P.; Dufr ene, Y. F. FEMS Microbiol. Lett. 2006, 264, 192–197.
(46) Nguyen, L.; Scherr, N.; Gatfield, J.; Walburger, A.; Pieters, J.; Thompson, C. J. J. Bacteriol. 2007, 189, 7896–7910.
(47) Takade, A.; Umeda, A.; Matsuoka, M.; Yoshida, S.-i.; Nakamura, M.; Amako, K. Cell 2003, 47, 265–270.
(48) Paul, T. R.; Beveridge, T. J. J. Bacteriol. 1992, 174, 6508–6517.
(49) Paul, T. R.; Beveridge, T. J. Infect. Immun. 1994, 62, 1542–1550.
(50) Paul, T. R.; Beveridge, T. J. Zbl. Bakt.: Int. J. Med. Microbiol.
1993, 279, 450–457.
(51) Chan, K.; Gascoyne, P.; Becker, F.; Pethig, R. Biochim. Biophys.
Acta 1997, 1349, 182–196.
(52) Zhou, X.-F.; Markx, G. H.; Pethig, R.; Eastwood, I. M. Biochim.
Biophys. Acta 1995, 1245, 85–93.
(53) Arnold, W. M.; Schwan, H. P.; Zimmermann, U. J. Phys. Chem.
1987, 91, 5093–5098.
(54) Gimsa, J. Bioelectrochemistry 2001, 54, 23–31.
(55) Pethig, R.; Jakubek, L. M.; Sanger, R. H.; Heart, E.; Corson, E. D.; Smith, P. J. S. IEE Proc. Nanobiotechnol. 2005, 152, 189–193.
(56) Hoettges, K. F.; Dale, J. W.; Hughes, M. P. Phys. Med. Biol.
2007, 52, 6001–6009.
(57) Johari, J. H.; Bner, Y.; Hull, J. C.; Dale, J. W.; Hughes, M. P.
Phys. Med. Biol. 2003, 48, N193–N198.
dx.doi.org/10.1021/ac2002017 Anal. Chem. 2011, 83, 3507–3515

Source: http://www.kirbyresearch.com/pdf/201109hawkinsAchem.pdf